La Raccomandazione del Consiglio dell’Unione europea del 22 maggio 2018 relativa alle competenze chiave per l’apprendimento permanente costituisce uno dei principali riferimenti normativi per l’insegnante. In una delle premesse iniziali il Consiglio lancia l’allarme sui livelli di competenza raggiunti dal cittadino, sia a livello globale sia europeo, negli ambiti linguistico, matematico, scientifico-tecnologico e digitale e specifica che “la memorizzazione di fatti e procedure è importante, ma non sufficiente per conseguire progressi e successi. Abilità quali la capacità di risoluzione di problemi, il pensiero critico, la capacità di cooperare, la creatività, il pensiero computazionale, l’autoregolamentazione sono più importanti che mai nella nostra società in rapida evoluzione.”
La capacità di risolvere problemi, in particolare, è centrale nell’apprendimento della matematica, tanto che il concetto di competenza matematica è sostanzialmente assimilato a essa: “La competenza matematica è la capacità di sviluppare e applicare il pensiero e la comprensione matematici per risolvere una serie di problemi in situazioni quotidiane.”
In linea con questa visione, le nostre Indicazioni Nazionali specificano che i problemi devono essere intesi come “questioni autentiche e significative, legate alla vita quotidiana e non solo esercizi a carattere ripetitivo o quesiti ai quali si risponde semplicemente ricordando una definizione o una regola.”
Per rispondere a queste esigenze normative, che vanno di pari passo con quelle didattiche, nella stesura del testo Tangram ci siamo ispirati a quelli che in letteratura vengono detti problemi ricchi (rich problems), cioè problemi che rispettano i seguenti requisiti:
- nel risolverli lo studente sviluppa le sue conoscenze matematiche;
- sono facili da capire e possono essere affrontati da tutti gli studenti;
- non posseggono una strategia risolutiva predefinita e conosciuta a priori dallo studente;
- sono percepiti come sfide, richiedono tempo e sforzo per essere risolti;
- possono essere svolti in diversi modi.
Per capire meglio di cosa si tratta, riportiamo un esempio di problema tratto dal volume 2B del testo Tangram, al termine dell’unità su circonferenza e cerchio.
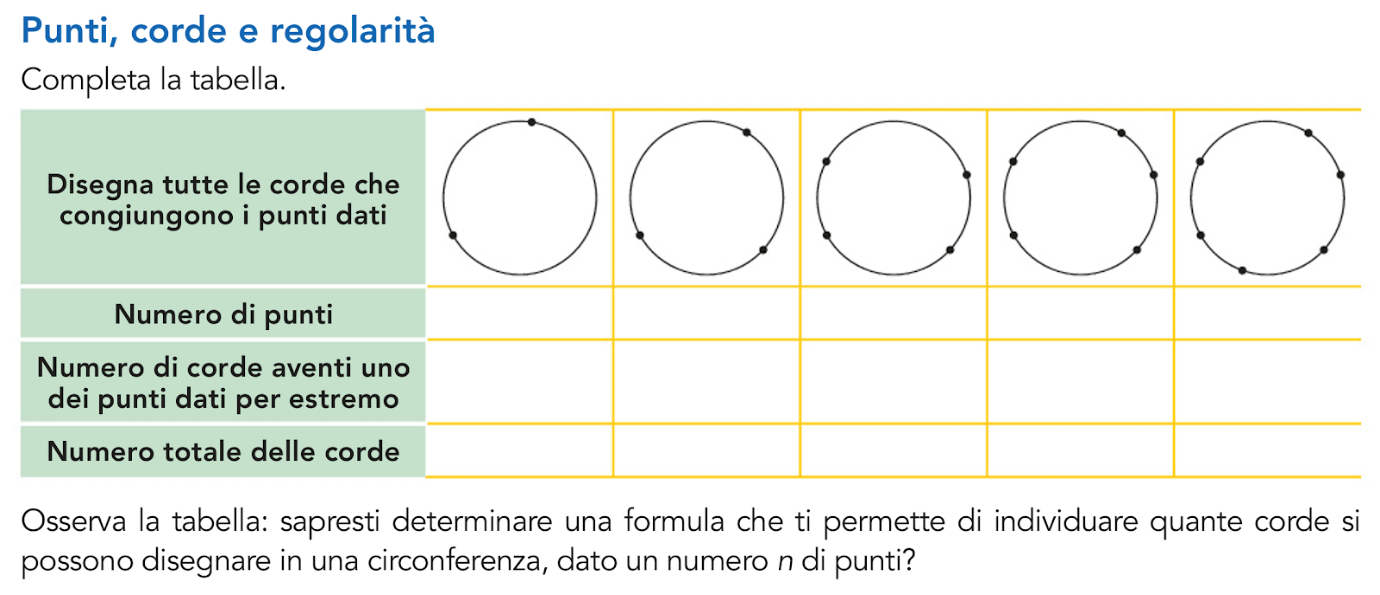
Vediamo perché il problema proposto può essere considerato “ricco”.
- Il problema parte da richieste molto semplici (tracciare le corde, contare i punti) ed è guidato passo per passo, è quindi accessibile a tutti.
- Lo studente non ha a disposizione tecniche o procedure che portino direttamente alla soluzione, ma deve formulare una strategia originale. Pertanto il problema richiede sforzo e tempo e viene percepito come sfidante.
- La formula generale può essere trovata in vari modi (ragionamento sulla figura; rilevazione di una regolarità nella progressione numerica; individuazione dei numeri triangolari, se già incontrati precedentemente) e si presta quindi alla discussione e al confronto tra studenti.
- L’attività di problem solving porta alla scoperta di fatti matematici nuovi, pertanto a un ampliamento delle conoscenze.
Concludiamo osservando che, benché le Indicazioni Nazionali evidenzino l’importanza dei problemi legati alla vita quotidiana, ciò non debba costituire un vincolo: il problema appena visto, infatti, sviluppa capacità di astrazione e generalizzazione che sono fondamentali per la costruzione del pensiero matematico e per il raggiungimento di livelli elevati di competenza.
Per approfondire:
- Scopri Tangram, il nostro corso di matematica per la scuola secondaria di primo grado, di L. Ferri, A. Matteo, E. Pellegrini – Fabbri Editore – Rizzoli Education, 2020.
- Raccomandazione del Consiglio dell’Unione europea del 22 maggio 2018 relativa alle competenze chiave per l’apprendimento permanente
- Indicazioni Nazionali, www.indicazioninazionali.it



